Disjoint Set

Definition

一個disjoint set維護一個"collection" $S = \{S_1,S_2,...,S_k\}$，並且以其中一個member來當作representative。要由哪個member來當作representative依據情況而定，如果沒有特別指明的話，collection中的任一member都可以是representative。

Operations

Disjoint set支援三個operation:

1. $Make$-$Set(x)$: Create一個新的set with x。
2. $Union(x, y)$: Union兩個set，然後產生一個新set。新的set的representative會是$x$, $y$中的某個member。
3. $Find$-$Set(x)$: 給一個member $x$，返回含有$x$的set的representative。

Implementation

Linkedlist

一個簡單的做法就是用linked-list來表示一個set。如下圖，每個set由一個linked-list來儲存，representative node的兩個pointer (head, tail) 指向第一個element和最後一個element，每個node也有兩個pointer，一個指向representation node，另外一個指向下一個element。

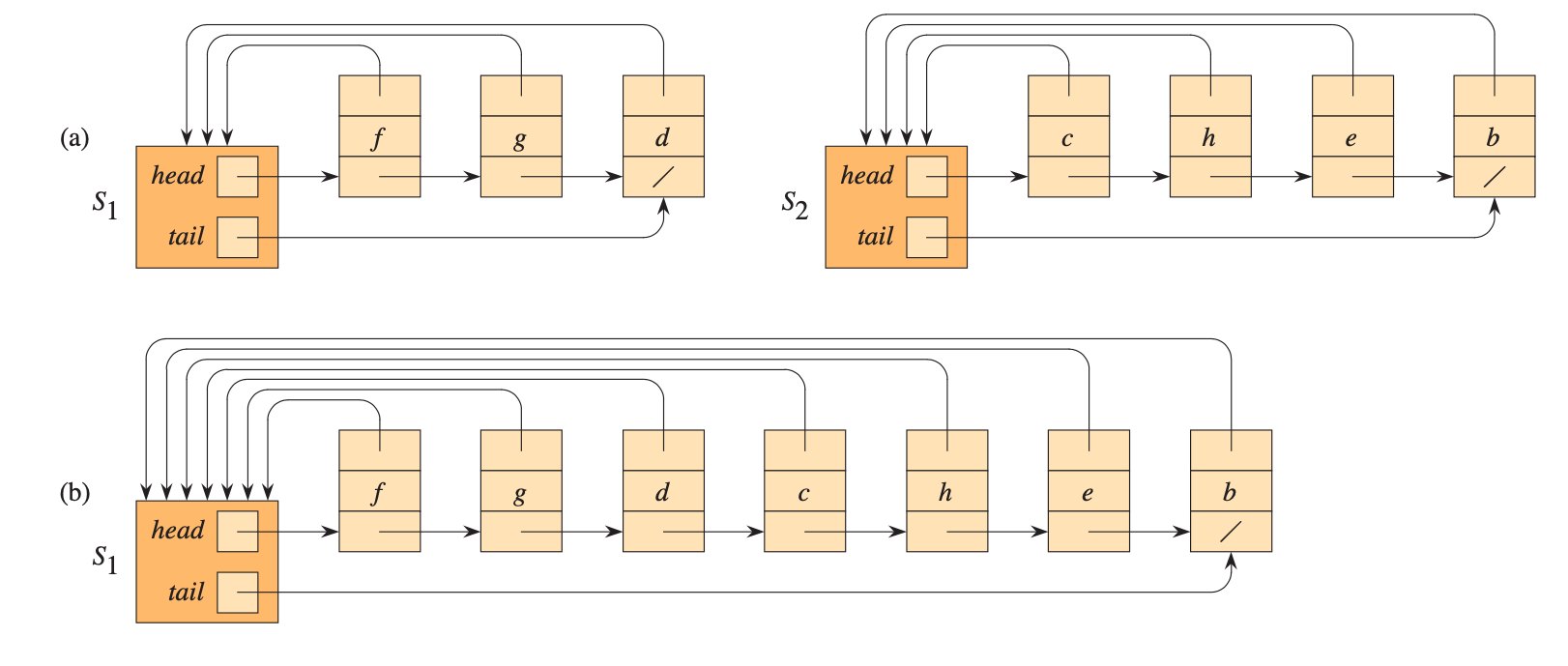
Make-Set(x): create一個linked-list只需要常數時間，因此 time complexity = $O(1)$

Find-Set(x): 每個node都有一個pointer指向representative node，所以time complexity = $O(1)$

Union(x, y): 當merge兩個linked-list，我們會把其中一個linked-list併進去另外一個，然後更新被合併linked-list裡面所有的節點，把representative pointer指向新的representative node。在這個情況，我們希望被合併的linkded-list是比較短的一邊，這樣要更新的節點數目比較少。我們可以採用weighted-union heuristic的做法，也就是reprensentative node同時紀錄節點數目，在合併時長的list合併短的數目。Time complexity = $O(n)$

Theorem 1

Statement: Using the linked-list representation of disjoint sets and the weighted-union heuris- tic, a sequence $m$ of $Make-Set$ , $Union$, and $Find-Set$ operations, $n$ of which are $Make-Set$ operations, takes $O(m+nlgn)$ time.

Proof:

因為有$n$個 $Maje-Set$的operation，所以最多也有$n$個set，這$n$個set的$Union$的operation的worst caset為每次merge都是差不多的長度，因此就是$n/2$, $n/4$, $n/8$...做merge，因此時間複雜度為$O(nlgn)$。

而有M個$Make-Set$和$Find-Set$ operation，每個的time complexity為$O(1)$，因此為$O(m)$，因此全部的時間複雜度為$O(m+nlgn)$。

Disjoint Forests

另外一種方式用tree來表示一個disjoint set，而這些disjoint sets就形成一個disjoint forest。

Make-Set(x): create一個tree只需要常數時間，因此 time complexity = $O(1)$

Find-Set(x): 每個node都有一個pointer指向parent，而representative指向自己，也就是root node，所以time complexity = $O(n)$ (tree是一條list)。

Union(x, y): 這種情況只需要把一個tree的root指向另一個tree的root，因此time complexity = $O(1)$。

Union By Rank

如果要改善$Find-Set(x)$的performance，就是樹的height越低越好，其中一個做法就是在union的時候，將矮的樹merge進高的樹，也就是rank by height。要做到這點，就必須要在root儲存目前樹的height當rank。

Path Compression

Path compression的做法是在$Find-Set(x)$的時候，順便把路徑上的每個node的parent都指向root，也就是把此顆subtree攤平。

Time complexity

利用union by rank和path compression的技巧，我們能得到$Find-Set(x)$ 時間複雜度為$O(m\alpha(n))$。而$\alpha(n)$是一個成長非常緩慢的函數，且$\alpha(n) \le 4$，因此可以視為$O(m)$，而$m$是operation的數目。

Golang Implementation

disjointset.go

type DisjointSet struct {
  Parent *DisjointSet
  Rank int
}

func (set *DisjointSet) Find() *DisjointSet {
  if set.Parent == set {
    return set
  }

  // path compression
  set.Parent = set.Parent.Find()

  return set.Parent
}

func (set *DisjointSet) Union(another *DisjointSet) {
  setRepresentative := set.Find()
  anotherSetRepresentative := another.Find()

  if setRepresntaetive.Rank <= anotherSetRepresentative.Rank {
    setRepresentative.Parent = anotherSetRepresentative

    // if the ranks tie, then anotherSetRrepresentative grows by 1 after merge
    if setRepresntaetive.Rank == anotherSetRepresentative.Rank {
      anotherSetRepresentative.Rank++
    }

  } else {
    anotherSetRepresentative.Parent = setRepresentative
  }
}